Related Rates | Volume Integration | Polar Calculus | Integration by Parts | Quiz
Related Rates
An application of implicit differentiation is through finding related rates. Finding a related rate means finding the rates of change of two or more related variables that are changing with respect to time.
Let’s take an imaginary, inverted cone with a height of h and a radius of r. Assuming that our cone is filled with liquid that drains its volume at a constant rate of x m2/s, we can figure out the rate of our liquid height’s diminishment is relation to the rate of the cone’s decreasing volume. However, we do need a few constants if we do not want our answers in terms of variables.
Example 1: Suppose you have an inverted cone (funnel) of radius 8 and height 6, which is filled to the brim with water. Through a small hole at the bottom of this funnel, water will leak out at a constant 3 m2/s. At what rate is the height of the water changing when the water is half as high as it started?
We start this problem off by finding an equation that related volume to height and radius for a conical shape. For this problem, we will use the equation
.
Because we want to find the rate of change for the height, and because we have no use for the radius, we can eliminate a variable by finding the radius in terms of height. When radius is 8, height is 6, so we can figure out that r=4h/3. We can then substitute this back into the original volume equation to get 
.By using the chain rule with implicit differentiation, we end up with the following when we differentiate our volume equation:
Now, all we have to do is plug in our given numbers from the initial problem. We can put in 3 m2/s for dV/dt, the rate of volume change. We can put in 3 for h, because we know that h at the instant that we want our rate of height change is at half the height of the initial condition of h=6. dh/dt will be what we are looking for, as that is that rate of change of h in respect with time.
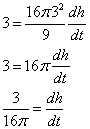
The rate of the change in height is 3/[16 π] m/s when the height of the water is half as high as when it started.
Example 2: Suppose you have a 6 foot tall man walking away from a light post that is 14 feet tall. The man walks at a constant 3 m/s. How fast is the tip of his shadow moving along the ground?
The man casts a shadow of length “x1” when he is a horizontal distance “x2” away from the light post. We can say that the distance between the shadow tip and the light post is “x” which is equal to x1 + x2.
By looking at the example, it seems that what we are solving for is dx1/dt. However, this is a common mistake. Note that the rate at which the tip of the shadow is moving along the ground is equal to the rate at which the distance between the tip of the shadow and the light post is increasing. Thus, we are actually solving for dx/dt.
The height of the man is 6 feet, so the distance between the top of the man’s head to the top of the light post is 14 - 6 = 8 feet. Now we have two triangles. One has legs of lengths 14 and x (also known as x1 + x2), and the other has legs of lengths 8 and x2.
We can see that these are similar right triangles, and we can set up the following equation:
(x1 + x2)/14 = x2/8
x/14 = x2/8
x = (7/4)x2
Now, we can implicitly differentiate.
dx/dt = (7/4)dx2/dt
We were given that the man is walking away from the light post at 3 m/s. This we can substitute as x2 because the rate at which he walks is equal to the rate the distance between him and the light post is increasing.
dx/dt = (7/4)(3)
dx/dt = 21/4 m/s
The tip of the shadow is moving at a rate of 21/4 m/s.