Related Rates | Volume Integration | Polar Calculus | Integration by Parts | Quiz
Parts Integration
Some functions cannot be differentiated using simple rules. Of the methods used to derive these more difficult functions, parts integration is one of the most crucial. Integration by parts requires splitting the equation into two parts, with each part assigned a variable of either u or dv.
Take the following equations for example:
![]()
![]()
The first equation can be broken in two as ex and sinx. It doesn’t matter which one we assign as u, or which one we assign as dv. However, the dx will always adhere to the split function that is assigned to dv. For example, if we want to assign ex as u, then our dv will be sinxdx. If we want to assign sinx as u¸ then our dv will be exdx. The same goes for the second equation, where one part could be x5 while the other part could be cosxdx.
To integrate by parts, subtract the integral of vdu from the product of u and v.
![]()
Example 1: ![]()
Let u = ex and let dv = sinxdx
Derive u to find that du = exdx. Integrate dv to find that v = -cosx. With our variables found, we can simply substitute our u’s, v’s, and du’s into the parts integration formula.

At this point, we can do parts integration again on the ![]()
We don’t want to undo our work by allowing our du become the new dv to be integrated, because then we will end up with ![]() . Thus, we will allow u to equal ex, and dv to equal cosxdx.
. Thus, we will allow u to equal ex, and dv to equal cosxdx.
Derive u to find that du = exdx. Integrate dv to find that v = sinx. We substitute all of this back into the equation. Don’t forget that we already have the original equation’s u and v.
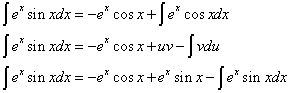
At this point, it seems as if we’ve fallen into the same situation, and that we have to do another round of parts integration. However, notice that you see ⌠exsinxdx on both sides of the equation, and that the only integrals in the equation are of ⌠exsinxdx. We can simplify the equation a bit.
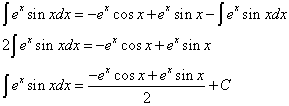
Example 2: Another way to integrate is by tabular integration. This method can be applied to any type of parts integration, but it is particularly useful when one of the parts of the equation can be eventually derived to zero. x5 would be an example of a part that can be eventually derived to zero, going from x5 to 5x4 to 20x3 to 60x2 to 120x to 120 to 0.
We will use the problem of solving ⌠x5cosxdx.
First, set up a 3-column table.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
On the first column, write alternating signs, starting from positive.
|
+ |
|
|
|
- |
|
|
|
+ |
|
|
|
- |
|
|
|
+ |
|
|
|
- |
|
|
|
+ |
|
|
On the second column, write your function on the first row, and its first derivate on the second row. Repeat while deriving further until that function reaches zero.
|
+ |
x5 |
|
|
- |
5x4 |
|
|
+ |
20x3 |
|
|
- |
60x2 |
|
|
+ |
120x |
|
|
- |
120 |
|
|
+ |
0 |
|
On the third column, write the cyclic function and integrate down the column.
|
+ |
x5 |
cosx |
|
- |
5x4 |
sinx |
|
+ |
20x3 |
-cosx |
|
- |
60x2 |
-sinx |
|
+ |
120x |
cosx |
|
- |
120 |
sinx |
|
+ |
0 |
-cosx |
Now that that has been completed, the integral is a simple matter of going down the column on a slant. Start at the left column, multiply this by the cell one to the right, then multiply by the cell one down and one right.
![]()
So obviously, the advantage to using the tabular method is that it's incredibly organized.