Related Rates | Volume Integration | Polar Calculus | Integration by Parts | Quiz
Polar Calculus
Differentiating polar equations.
Since most of our functions will be given as R(theta), it takes additional steps to find the slope of the tangent line since we want dy/dx. To find dy/dx, we can first find dy/dtheta and then divide by dx/dtheta, effectively leaving dy/dx.
Example 1: Find the slope of the line tangent to 
at 
Since we want to find 
, we will need to find 
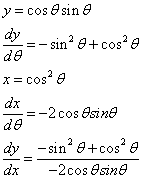
Now we substitute in 
and find that 
, when .
Finding areas of polar equations.
Unlike finding the area in a cartesian system, finding the area in a polar system means that the area will be a sum of the sectors swept out instead of a sum of rectangles.
To find the area over an interval (a,b) it is 
.
Example 2: Find the area of the region 
Since the period of this function is just 
, we can simply integrate from 0 to .
